数据分析应用实战:阳台能晒多长时间太阳?
来源:广东 CPDA数据分析师 / 作者:刘程浩 / 时间:2020-10-12
前段时间比较忙,我和老婆差不多在第N时间才加入现在所在小区的住户微信群。感慨一下,现在不同于几十年前住单位福利分房了,那时候串门联络感情非常方便。那时候大家都在一个大单位工作,住的都是同一个单位的单身汉或者家属,平时白天都可以不用关门,打招呼串门很方便。而且那个年代职工新搬进单位的宿舍,提着一篮子熟鸡蛋遛一圈,就能把所有邻居都认识了。
但在商品房+微信的时代,邻居们都来自五湖四海,平时都不怎么见面。要想熟络一下,认识认识同一楼层的邻居都不一定有时间。但我发现,微信群里共同聊一个话题,倒是个不错的熟络方法。
今天上班路上,就看到群里正在热烈讨论一个话题,“我家的阳台能不能晒到太阳,或能晒多久的太阳?”如下图,里面不乏许多大神级的解读。
阳台要有太阳晒,这是个很老题材的话题了,其实在看房阶段,决策是否要买这个单元之前,怕是大家都已经在楼盘工地、样板间里来回穿梭,考察好几十回了。但由于很多房子是预售,看的时候还是工地,真正搬进去的房子在那个时候不仅进不去,且房子周围都是脚手架和堆满的建材,比较危险。因此很难真实的考察到很多细节,多远远地看一下楼距,估计一下自己看中的房子有多高。
如果说一开始买的楼层很高,或者买的是小区边上户型,那这个问题就不是问题,因为确实没有小区内其他的楼宇遮挡自己的阳台采光。而其他楼层的户型就不同了,如果来看房的时候赶上阴天,或工地正在施工进不去……所以很大程度就要看经验或者自己预判。
当然了,有门路的可以找熟人咨询;而没有熟人的,那就只好在样板间、售楼大厅研究模型,或者研究下售楼书上的宣传图纸。
等掰着手指可以验房和交房的时候能走进屋里看了,大家会发现很多细节和之前看到的模型和图纸多少有些出入。甚至时间久了,看到真正房子时,却又记不得当时考虑的因素。
因此,要想回答自己家里的阳台一年下来每天能晒个多长时间,还是要重新考虑和计算的。下面介绍3种比较常用的方法:
方法一:实地测量和计时法
由于在北半球,考虑到每年的夏至、冬至是一年中白天时间长和短的两个特殊日子,因此可以在那2天专门在家测算和观察下,太阳有没有照进阳台,照进来多大面积,一共照了多长时间,非常精准。其余的日子里,阳台被光照射的时间就是这2个日子观测到的中间值。非常简单对吧?不过用这种方法,对于大多数年轻人来说,还是有一些比较严格的条件:
1、一般来说你得比较有时间(例如财务自由),或者已经退休在家,总之来说得比较有时间。因为夏至和冬至这2天,遇上周末不用上班的可能性不大。比方说今年的夏至,就是星期一得上班。如果不是财务自由或退休在家,你总不能和老板或者和客户请假,要待在家里看太阳吧?所以,比较有时间的人,才能够用得到这种方法。
2、得天公作美,或者说天气得配合。如果夏至那天刚好遇上大暴雨或阴天,冬至那天刚好下雪或也是多云,你就没法去观察和测算了。再加上这2个时节,下雨或阴天,经常一搞就好几天,你也说不准哪天请假方便。难道你敢请假一请就请个一星期,不至于吧。
3、当然还有一种互联网的方法,那就是家里安装摄像头。很多人的家里都装了摄像头,不过很多人的摄像头都是拍摄室内。因此,除非阳台上装了一个摄像头能够拍摄到下来阳台的光照情况,这样就可以通过在家里回看视频统计太阳晒阳台的时间了。
方法二:卫星图片观察法
如果你有能看到卫星图片这方面的人脉,那就太方便了。只要调出夏至和冬至的卫星图片(或者之前之后几天的,只要是晴天的都行),看看太阳照射下,自己住的楼层没有被其他楼层的影子遮挡的时间有多长就行了。当然,还有更加先进的图像处理算法,可以在雨天模拟出晴天的效果!这种人脉资源怕是相当的难得,因为一般来说,只能找商业卫星公司。如果你没有这方面的人脉,还有一种大致估计的方法:自己可以下载谷歌地球,在谷歌地球上可以根据时间线找到靠近夏至和冬至这2天的卫星图片,然后观察下自己住的楼层没有被遮挡就大概知道了。
例如,我找到了深圳的著名建筑京基100,和它旁边的荔园酒店。这张照片拍摄于2020年3月16日早上8点,从京基100的影子上可以推算在春分8:00的时候,京基100的影子大概率是不会对荔园酒店的底层构成遮挡的。既然春分时节都不会遮挡,那么夏至日早上8:00更加大概率不会遮挡。而冬至日嘛,这个还不太好说。
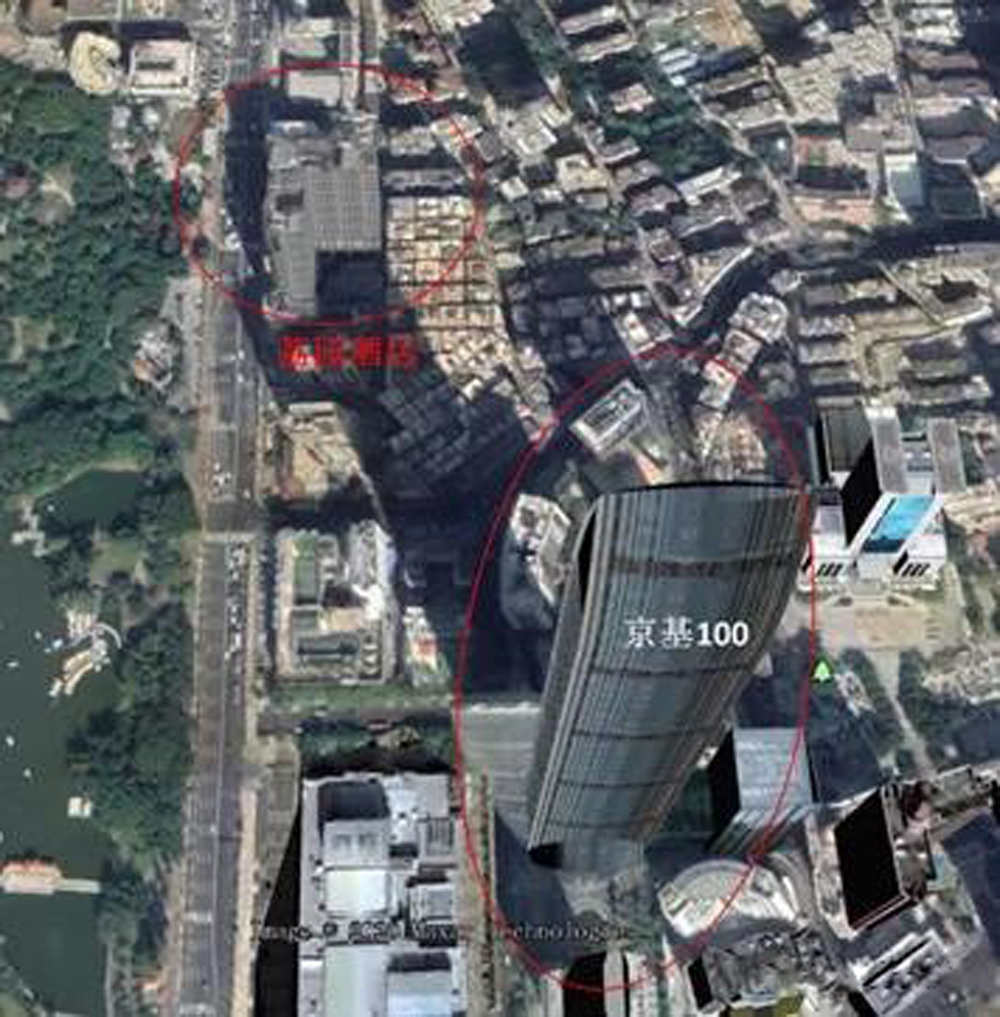
因为这种方法,还是有些问题:
1、谷歌地球的照片不是每天、每时都更新的,因此想要看到更加详尽的照片,特别是具体某一点某一时刻的照片,真得比较难;
2、这种通过影子的估算和估计,需要读图人有一些比较基础的看图能力和地理学知识。不然,影子往哪里偏移,影子在偏移的过程中该做多少压缩或延伸,如果都没个概念的话就麻烦了。
方法三:太阳高度角方法
我们考虑一般化场景:如下图,一般来说如果能够住在左边建筑的A点或以上位置就是不错的,因为A点不容易被对面建筑的影子遮挡,而住在B点的话会被遮挡。但对于住在C点而言,到底会不会晒到太阳呢?
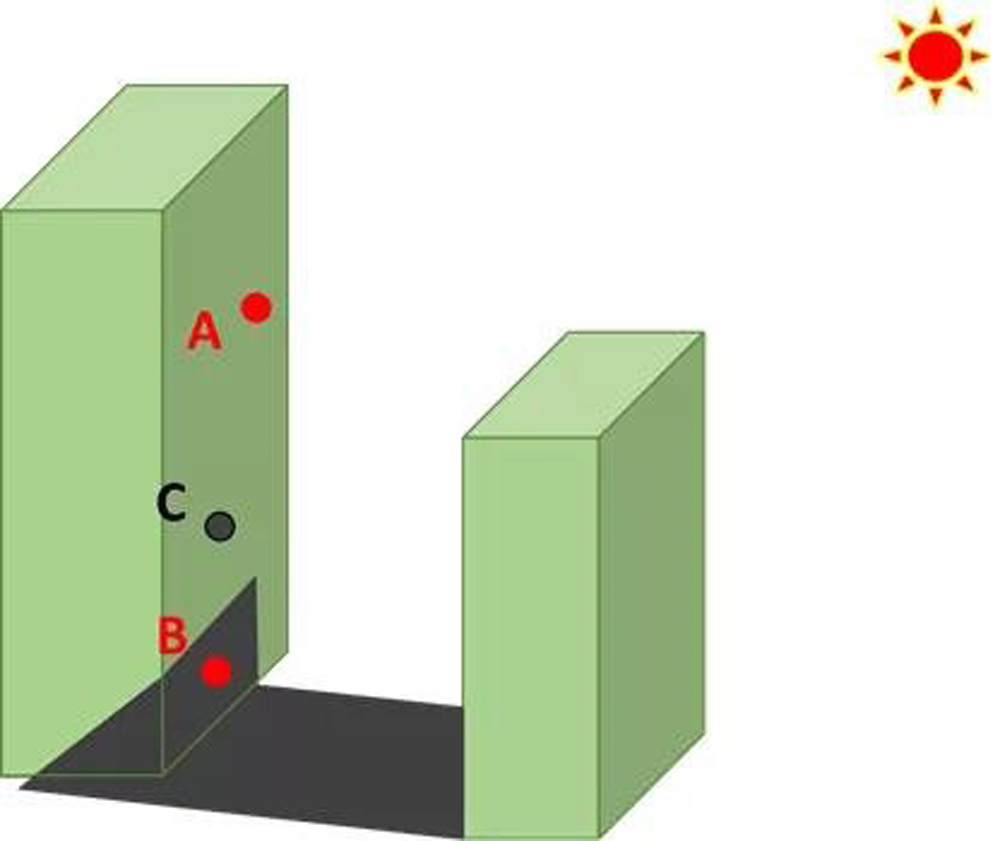
为此,如果选用太阳高度角这种方法就会比较复杂,需要一定的地理学或天文学的知识,以及几何、三角函数的基础。所以,我建议只要时间充足,可以考虑方法一;家里有矿可以考虑方法二;像我这样平时比较忙,又只能搬砖挖矿的,就倾向于方案三了。
回到正题,方法三的思路从下图看出要从2个切入点入手:
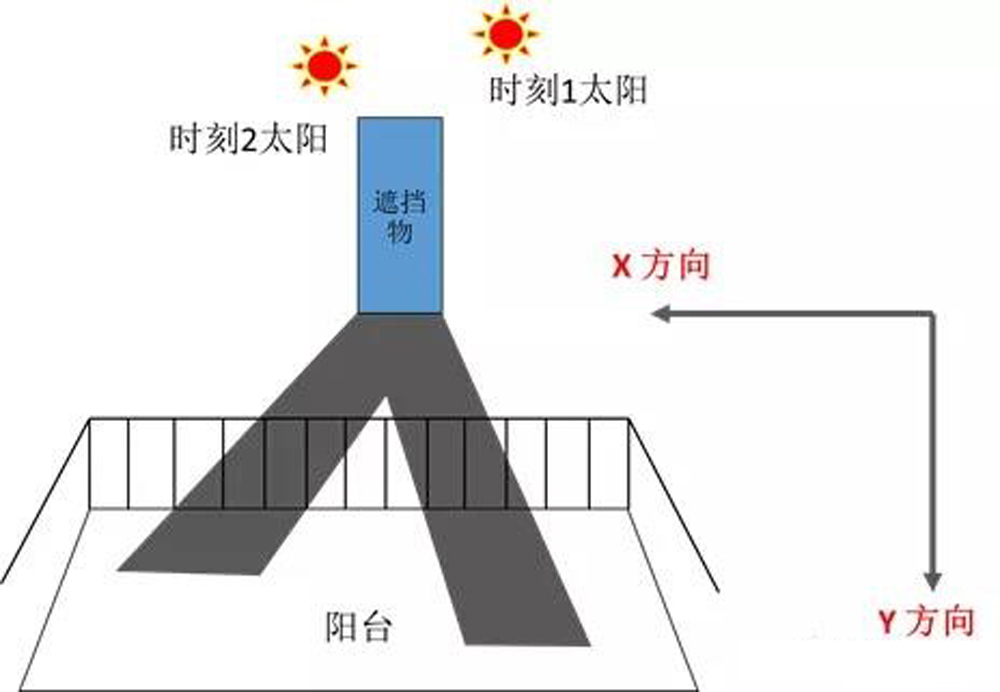
假设你站在阳台上,阳台对面有个遮挡物会造成阳光的遮挡,从而在阳台上落下影子;不同时刻的太阳位置,落在阳台上的影子的位置是不一样的;
个切入点,Y方向作为0-1的先决条件:由于阳台比较窄,因此只要阳台出现影子,就说明被遮挡1,反之就不被遮挡0;第二个切入点,一旦阳台被遮挡,那么X方向上长的影子移动距离是多少?
下面先研究Y方向,阳台是否会被遮挡
从中学的地理知识可以知道,北半球两栋建筑物之间的距离,至少要保证在冬至日的正午时刻,相互间不产生阳光遮挡。为啥这么说呢?
、正午时刻太阳高度角在中,此时影子短。如果正午时刻对方建筑被自己的影子所遮挡,那么当天其他时刻,自己的影子都大概率会遮挡住对方(考虑到对方建筑可能较宽,所以用“大概率”);
第二、冬至日那天,太阳直射点在南回归线,北半球太阳高度角在一年中所有的正午时刻中是的。如果这的正午对方建筑被自己的影子所遮挡,那么一年到头所有的日子,大概率下自己的影子都会遮挡住对方。用下图来表示就是这样:
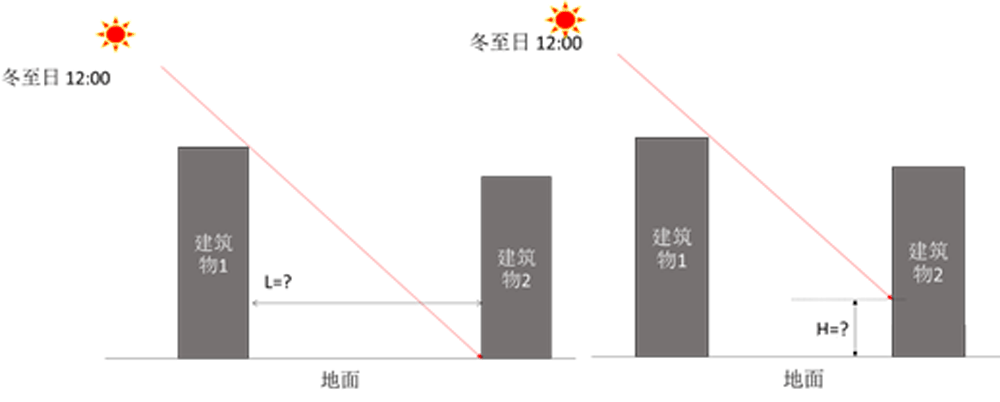
在上图左中,冬至日12:00时,如果那条红色的光线刚好照到了建筑物2的墙角,此时两栋建筑物的距离L,就刚好是建筑物2不被对面建筑1影子遮挡的小距离。这个时候,只要建筑物2距离建筑物1的水平距离≥L,那么至少全年的正午时刻,在建筑2门口肯定能晒到太阳。
可是现实中很多时候,如上图右,开发商为了节省用地,两栋建筑物之间的距离会小于L。或者说考虑到1楼和2楼作为入户大堂不住人,照不照太阳影响不大,因此允许两栋楼之间的距离小于L。
此时,上图右的问题就变成H= ?时,在这个高度以下的建筑物长时间晒不到太阳。
为了回答L =?以及H =?我们用一个场景进行建模,选择下图中建筑1和建筑2作为研究对象

步,需要判断的是,太阳到底出现在建筑1一侧,还是建筑2一侧。因为太阳的位置将决定谁会被遮挡住。
这一步的判断其实不难。
首先看上图,由于是拍摄于2019年11月8日早上11:00,此时建筑物的影子方向朝北,此时说明太阳就在南方,因此太阳的位置就在建筑1那侧。
还有一种方法就是考察纬度的因素。
我查了一下所在的韶关市市区的地理坐标,大致是N 24.8°,E113.8°。
由于在11月份,太阳的直射点在南半球,而韶关市在北回归线以北,因此也可以看出,太阳靠南,在建筑1那侧。

这样一来就清楚了,建筑1和建筑2之间,我们要考察的是建筑2是否会被建筑1的影子所遮挡。
第二步,简化建模,考察一下建筑1和建筑2之间的距离L是否达到了互不遮挡的小值?
这时候,我们将建模所需要的参数,放到图中来看就比较清楚了。
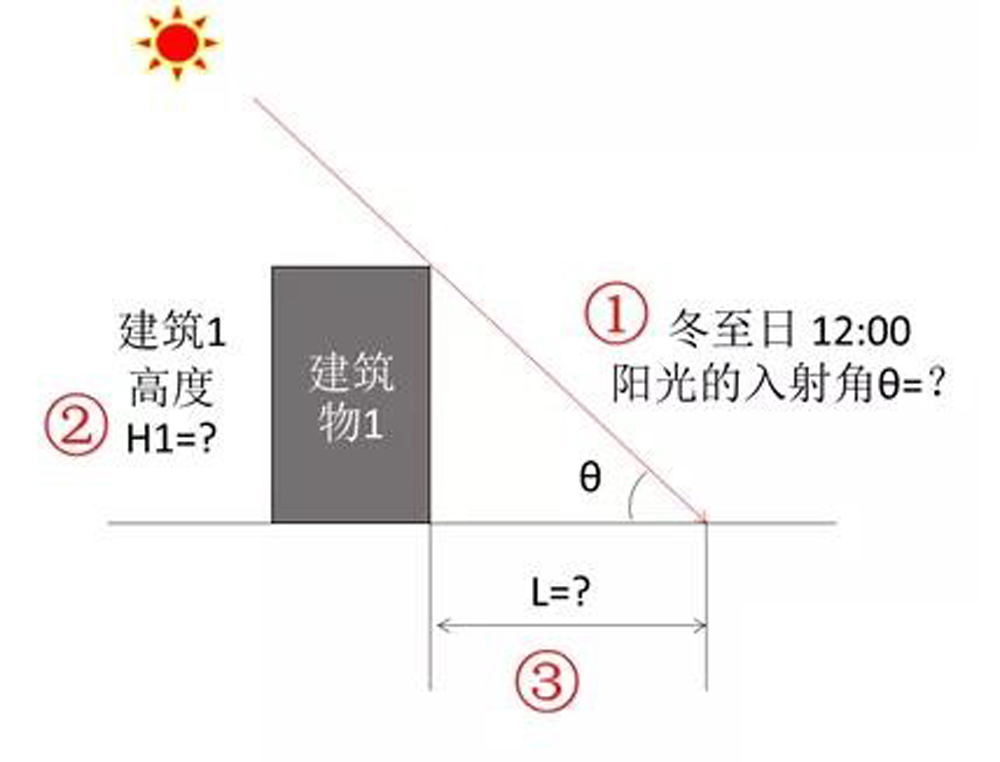
上图中一共有3个参数:
参数1,冬至日12:00,阳光的高度角θ=?
参数2,建筑1的高度H1 =?
要求出的参数3:此时建筑1的影子长度(或者小楼距)L=?
首先求θ,这个容易求出来 θ=41.7°。一般的,天文学中关于某天某时刻的太阳高度角的计算公式是这样:
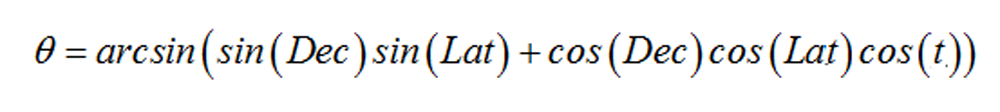
上面的等式中,Dec:赤纬,天文学术语,指的是太阳直射点的纬度,如果在南半球则取负数。冬至日太阳直射点在南回归线,也就是取Dec = -23.5°
Lat:观测点所在的纬度,例如韶关的纬度就是N 24.8°。
t:时角,天文学术语,解释起来有些费劲儿,百度百科是这么解释的:天体的时角定义为天子午圈与天体的赤经圈在北极所成的球面角。换成不太严谨但容易理解的话说,就是地球每个小时自转15°,在观测时点上,地球已经自转了多少个15°。
计算公式是 t =(观测时点-12)×15°
例如,现在是正午12点,那么时角就是0°,之所以要减12,那是因为规定了正午12点的视角为0°的缘故。不过由于取的是正午时间,因此cos t=1,整个公式就简化了。经过数学变形,得到冬至日正午时刻韶关市区的太阳高度角为θ=π/2-(Lat-Dec),也就是41.7°。
用高中课本中简单的平面几何公式就可求出。
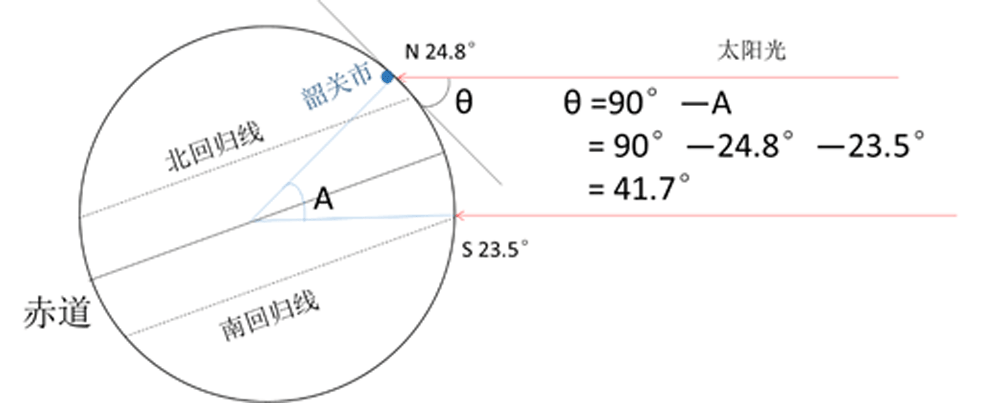
其次求H1
求H1的方法有很多种。高手都在民间,所以我就用了一种相对容易的方法。
工具是激光测距仪,原理用的是勾股定理。
原理和实操都很简单,下图大家一看就秒懂
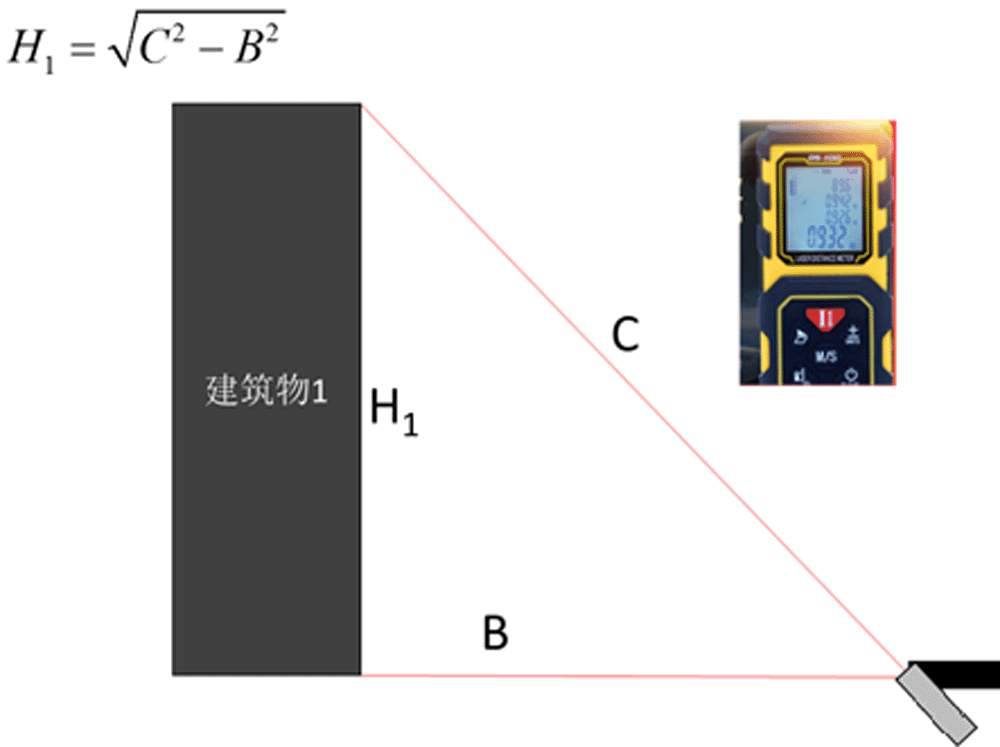
求出了θ,H1后,那么L就容易求了利用公式:代入数值求出L;
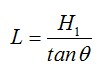
在进入下一个环节之前,我们不妨根据一般性推导出一个临界公式,也就是测算当在建筑2所住的楼层阳台顶部外沿高度要达到的临界值(见下图)。

经测算,一般情况下,H的临界值为H临界=H1- L1×tan(θ)
当阳台顶部外沿实际高度高于临界值H临界时,至少能保证每天正午能晒到太阳(也就是Y方向判定不被遮挡),此时可以测算出在冬至日那天能晒到多久的太阳;当阳台顶部外沿实际高度低于H临界时(Y方向上判定被遮挡),那就一年到头大概率会晒不到太阳。
下面研究X方向上,影子横向移动多宽
这个就比较需要系统的立体几何以及天文学的基础知识了。总体的研究思路流程如下:
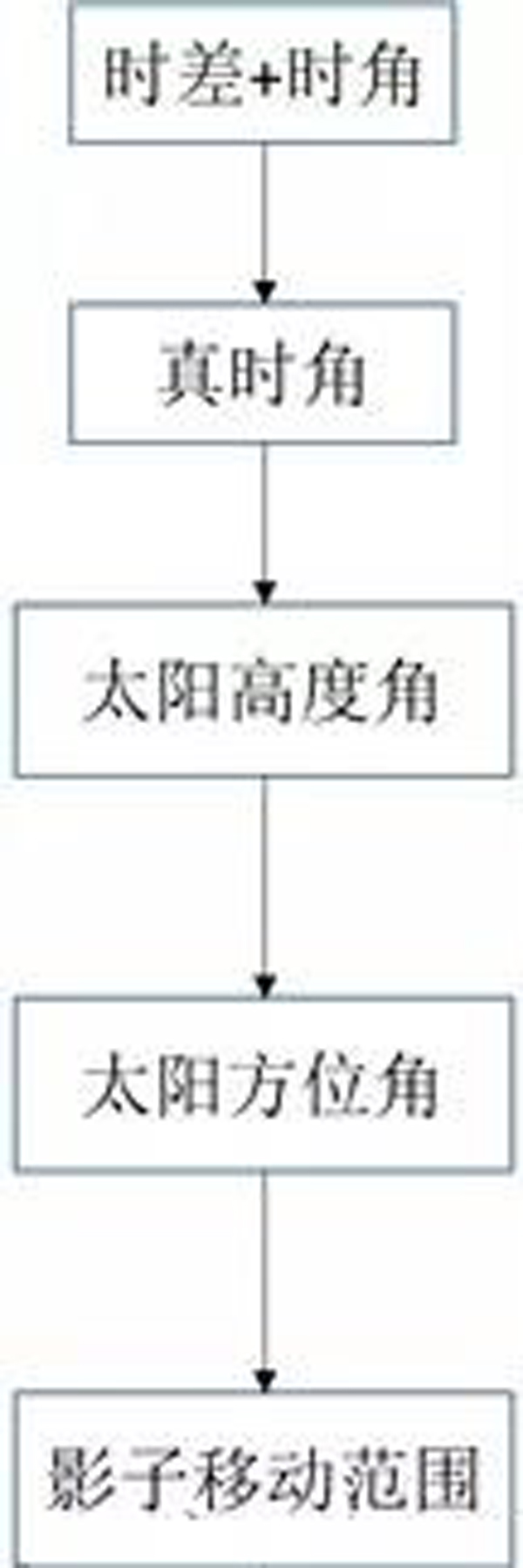
上面的流程中,有一些名词已经之前解释过了,这里不多做解释;下面讲一下没介绍过的。
1、时差:不是旅游倒时差的那个时差,而是标准时区的经度和观测地的经度之间存在角度距离。例如北京时间所在经度为E 120°,而韶关经度为E113.6°,相隔了6.4°,从时间上看差了大约半个小时。也就是说当北京时间早上6:00的时候,韶关真正的时间是早上5:30多一些。之前写太阳高度角的时候,按道理也要考虑这个因素的,但一方面前面内容不用涉及到太阳升起和日落,另一方面误差也不大,因此就没在之前考虑了。时差的计算公式为:
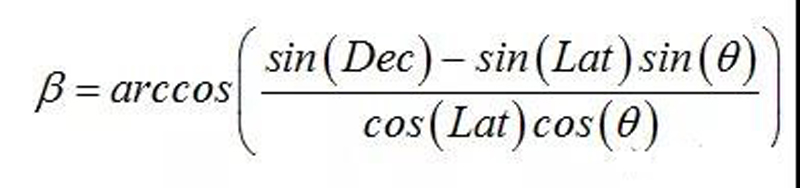
这个看着不太好理解,下面我画个图大家就容易理解了。
首先,由于存在时差,韶关的冬至日是要到12:26分,太阳才到达正南方,此时影子短。此时的太阳高度角为41.7°,太阳位于正南方,此时方位角为β= 180°;其次,同样因存在时差,冬至日早晨是7:12分日出,17:40分日落。经计算当天太阳是在正南方偏东约64°升起,也就是俗话说的约东南方升起(此时β=-116°,负数代表上午。但是站在观测者的角度上看,负数度数看着很别扭,所以取|β|的补角64°,就会比较自然和生活化);同理,当天太阳在正南方向偏西约64°的方向落下,即俗话说的约西南方向落下。
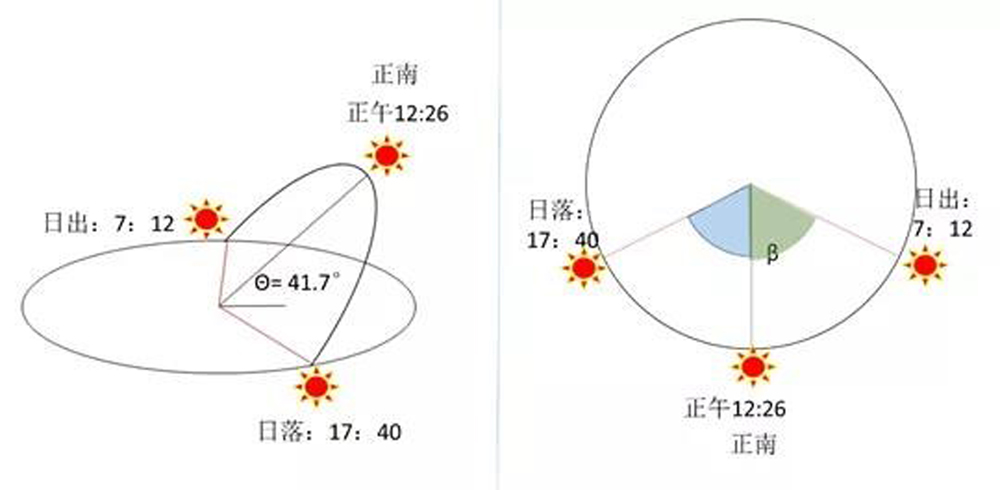
太阳方位角的变化,就决定了影子的活动范围
4. 影子活动范围,指的是太阳在不同的方位角出现时,影子的位置。在这里,我们需要确定一个时间范畴。理论上一旦太阳出现在地平线之上,只要有遮挡物就一定会有影子,但有些时段的影子我们并不care。例如我们想晒衣服,早上10点之前的太阳,阳光并不强烈,此时晾干的贡献比晒干还大;亦或者傍晚时的太阳,也是如此。只有日上三竿到正午,正午到下午那段时间的太阳是我们生活中所需要的。所以我们想要研究阳台能否晒到太阳或者能被太阳晒多久,应该取一个我们都常用来晾晒的时段,在这里我就取上午10:00到下午16:00。
我计算了一个韶关市区冬至日不同时段的太阳高度角-方位角一览表。一起来看一下(第二列粘贴时发生错误,请忽略)
|
时点 |
太阳高度角θ |
生活化的方位角 |
|
10:00 |
1. 18° |
南偏东39.15° |
|
11:00 |
1. 46° |
南偏东25.06° |
|
12:00 |
1. 36° |
南偏东7.95° |
|
12:26 |
1. 7° |
正南方 |
|
13:00 |
1. 07° |
南偏西10.36° |
|
14:00 |
1. 66° |
南偏西27.13° |
|
15:00 |
1. 01° |
南偏西40.78° |
|
16:00 |
1. 19° |
南偏西51.35° |
有了这个表,并基于表中的数据我们就可以制作一下3个关键时点的影子变化边界,我将这3个时点的影子的边界连接上去后,得到了下图的2条虚线。
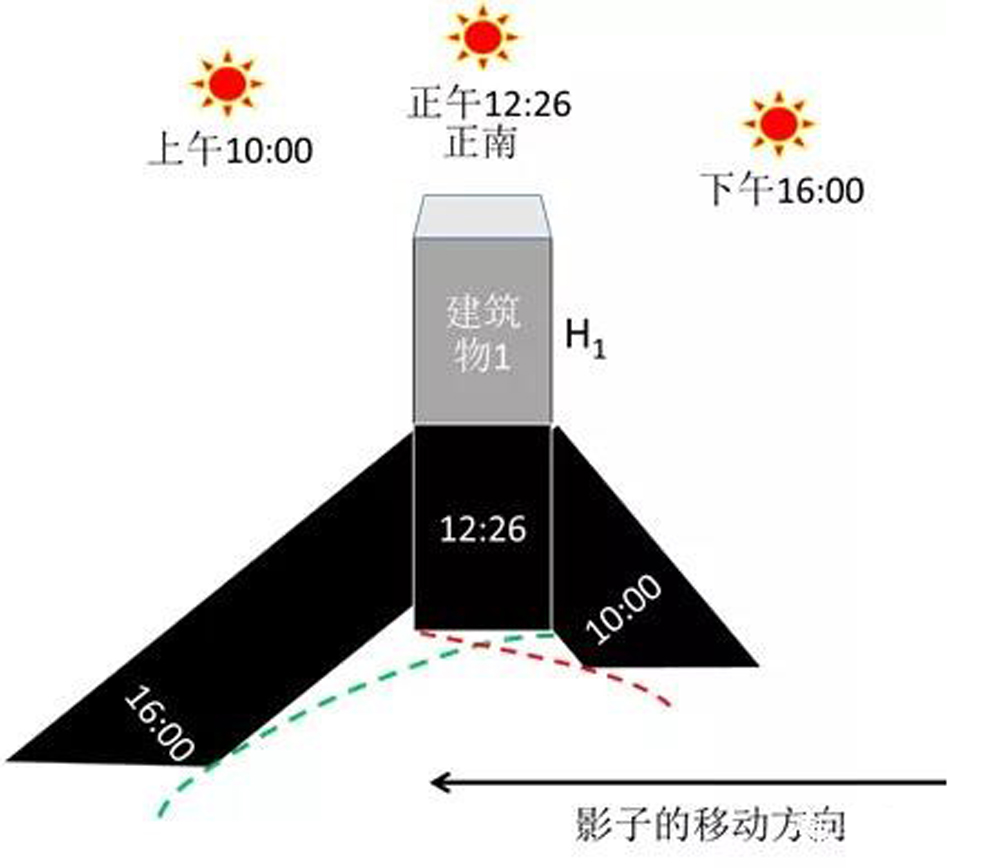
如果你住在1楼,若从10:00到12:26,阳台位于红色虚线之下(外),或者下午12:26-16:00,阳台位于绿色虚线之下(外),那么阳台都是可以晒到太阳的。1楼晒得到太阳,那么1楼以上的住户肯定全都晒得了太阳。但实际上经常是这种场景,那就是受之前所说的楼距过小的影响,没办法住在上面2条虚线范围之外。这个时候我们就回到之前讲到的一般化场景。
我们想知道下图中C点(假设为阳台的顶部),从10:00到16:00之间是否能够晒到太阳?这个就要花点时间来测算了。
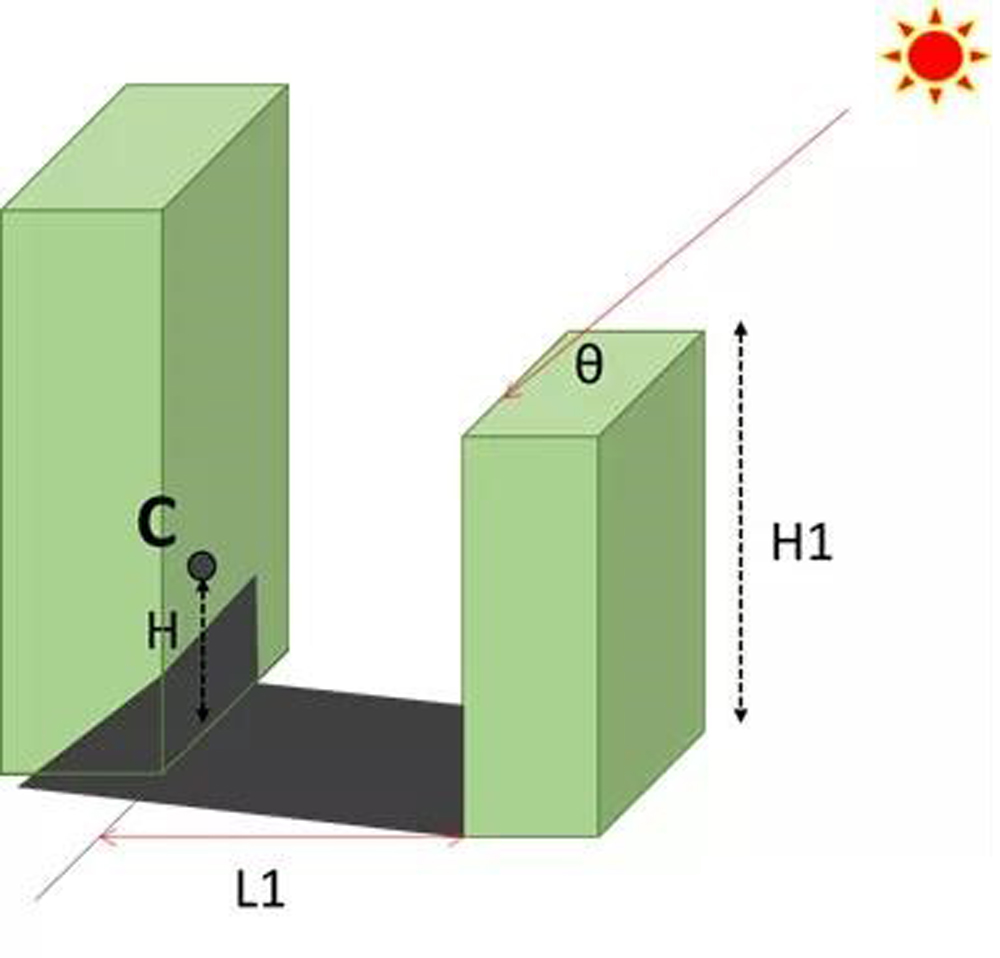
关于C点能否在冬至日正午晒到太阳,从前面推导出来的先决条件H在正午时刻的临界高度值H临界正午 = H1- L1×tan(θ正午) 计算出的H临界正午,如果这个值≤H,那么C点在冬至日正午肯定可以晒到太阳。至于早上10点到下午16:00能否都能晒到太阳,则还需进一步分场景计算。
有一点可以肯定的就是,中其他时间点的太阳高度角肯定比正午时θ值要低,这就意味着除正午外其他时间点的影子上沿高度肯定超过H临界正午值。这个是显而易见的,如下图:影子越长,一旦影子受到遮挡,影子的上沿就越高。
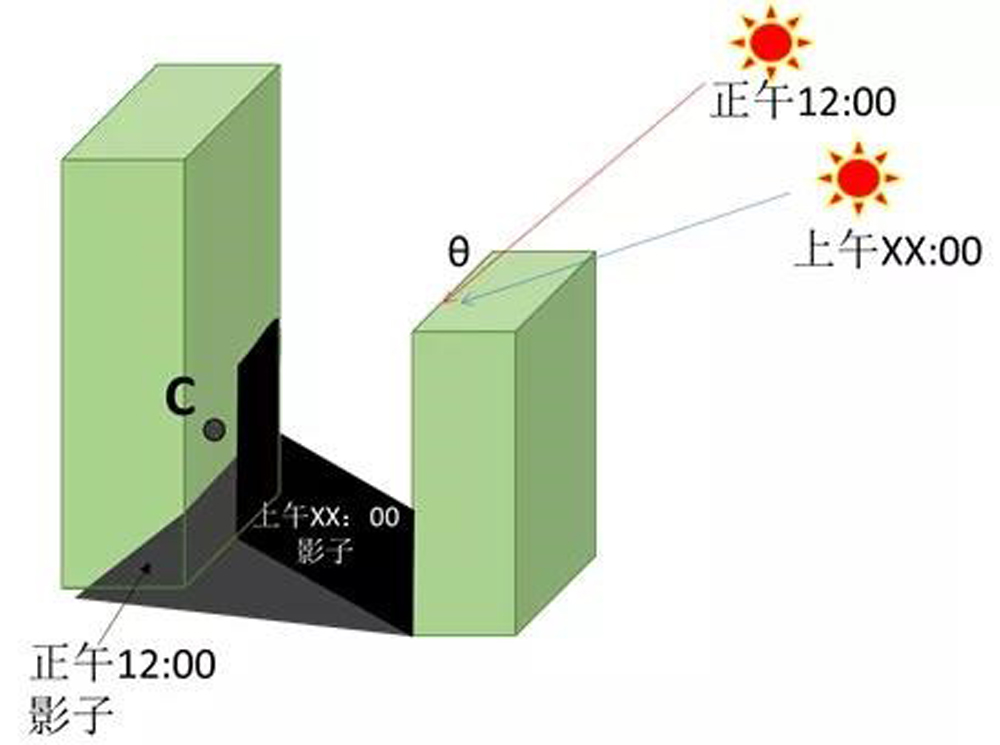
于是,我们得到一个判断C点是否被影子遮挡的临界条件状态,不过所需要要换成具体的场景来看。首先C点是阳台的天花完整外沿,它是有长度的。我们设左侧为C1,右侧为C2,每天影子的变化方向是由C1→C2,也就是自西向东。

另外,当我们把分析的视角从轴测图转向平面图时,就很容易分析了。下图中,是代表冬至日当天,上午10:00到正午12:26分时,需要测量的量包括如下:
上午的太阳方位角β0
C1点和对面建筑外立面构成一个夹角β1,C2点和对面建筑外立面构成一个夹角β2,由下图易知,β1 > β2
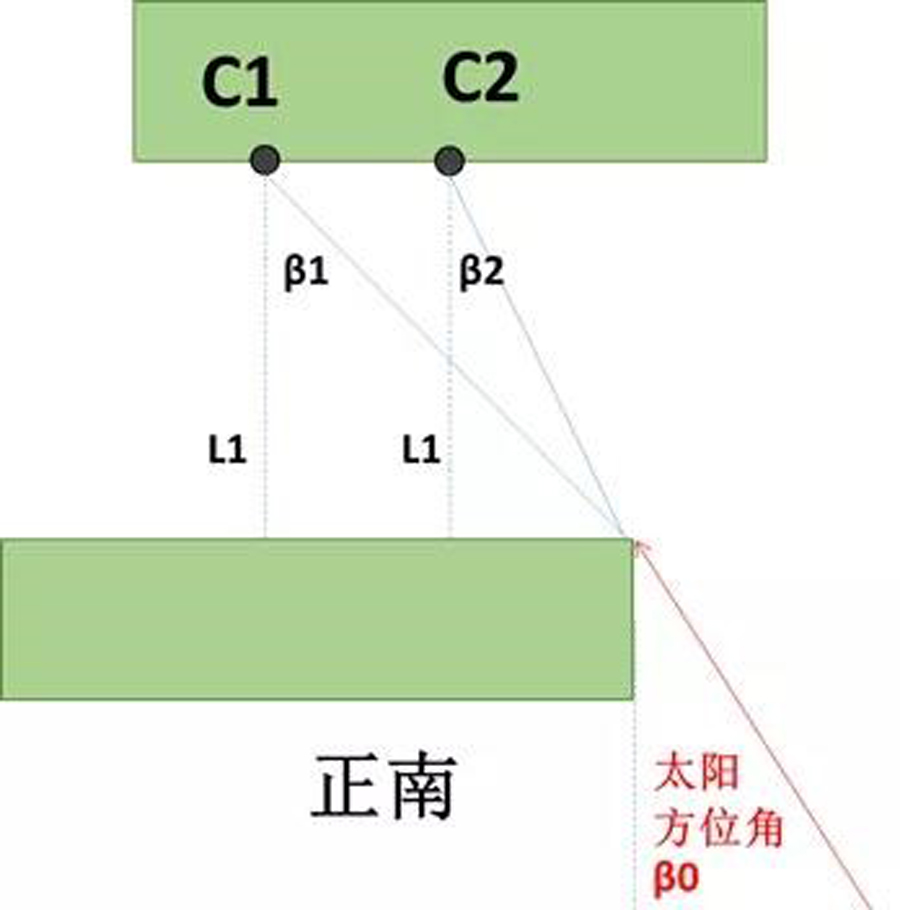
β0、β1、β2之间存在如下关系:
当β0 > β1时,整个C点阳台不受遮挡;
当β2 <β0 ≤β1 时,C点阳台开始被遮挡或部分被遮挡,此时还要兼顾H和H临界。这个时候,如果在此期间H≤H临界,只要逆运算β1和β2分别等于太阳方位角时的时刻,就知道C点阳台被影子遮挡的时间;如果此期间H≥H临界,则C点阳台完全不受遮挡;
当β0 ≤β2时,如果在此期间H≤H临界,C点阳台完全受到遮挡;如果此期间H≥H临界,则C点阳台完全不受遮挡;
同样的,如果是在下午这段时间内
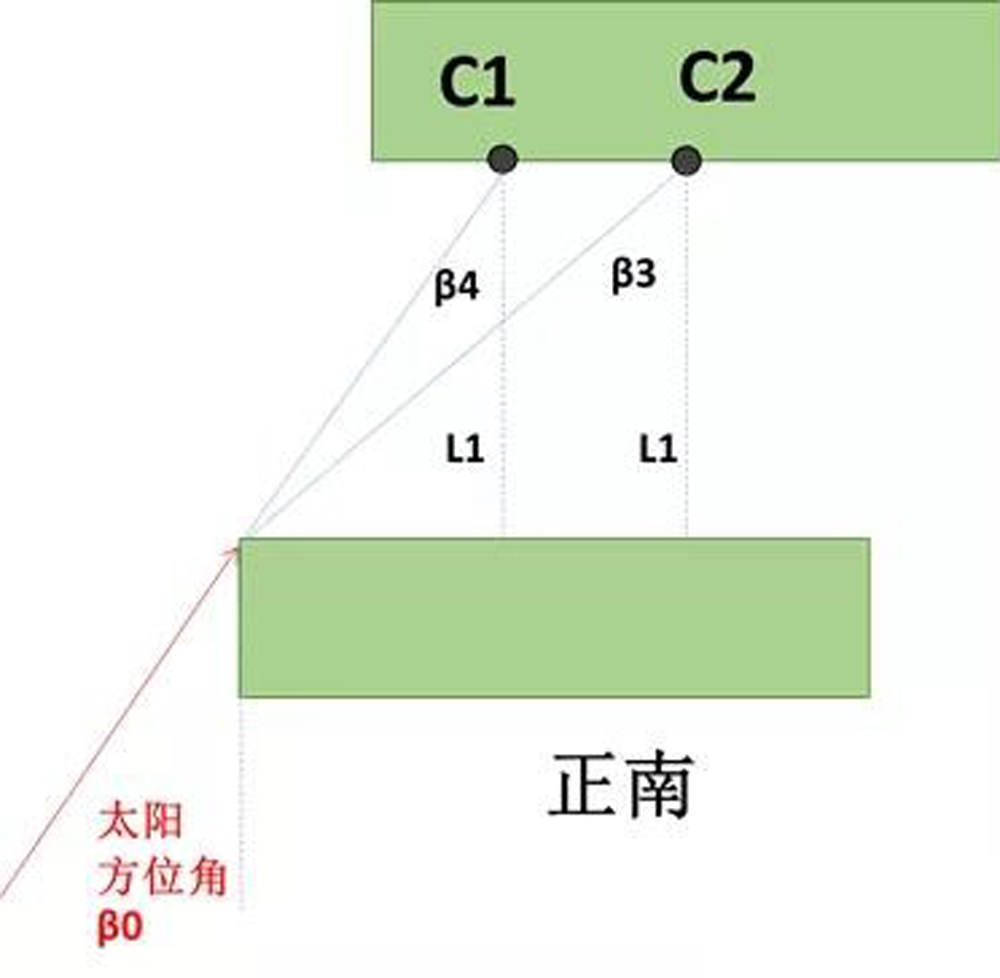
β0、β3、β4之间存在如下关系:
当β0 >β3时,整个C点阳台不受遮挡;
当β4 <β0 ≤β3 时,C点阳台开始被遮挡或部分被遮挡,此时还要兼顾H和H临界。这个时候,如果在此期间H≤H临界,只要逆运算β3和β4分别等于太阳方位角时的时刻,就知道C点阳台被影子遮挡的时间;如果此期间H≥H临界,则C点阳台完全不受遮挡;
当β0 ≤β4时,如果在此期间H≤H临界,C点阳台完全受到遮挡;如果此期间H≥H临界,则C点阳台完全不受遮挡。
分析了那么久,举个实例分析下:
假设小王住在在韶关市某小区,他所住的楼层阳台顶部外沿距离地面28米,他的阳台的南面斜侧,有另一栋小区住宅楼,楼高40米。小王所住的楼和阳台对面的楼楼距为 20米,对面楼的立面和小王阳台顶部外沿的两端,形成的夹角如下图:
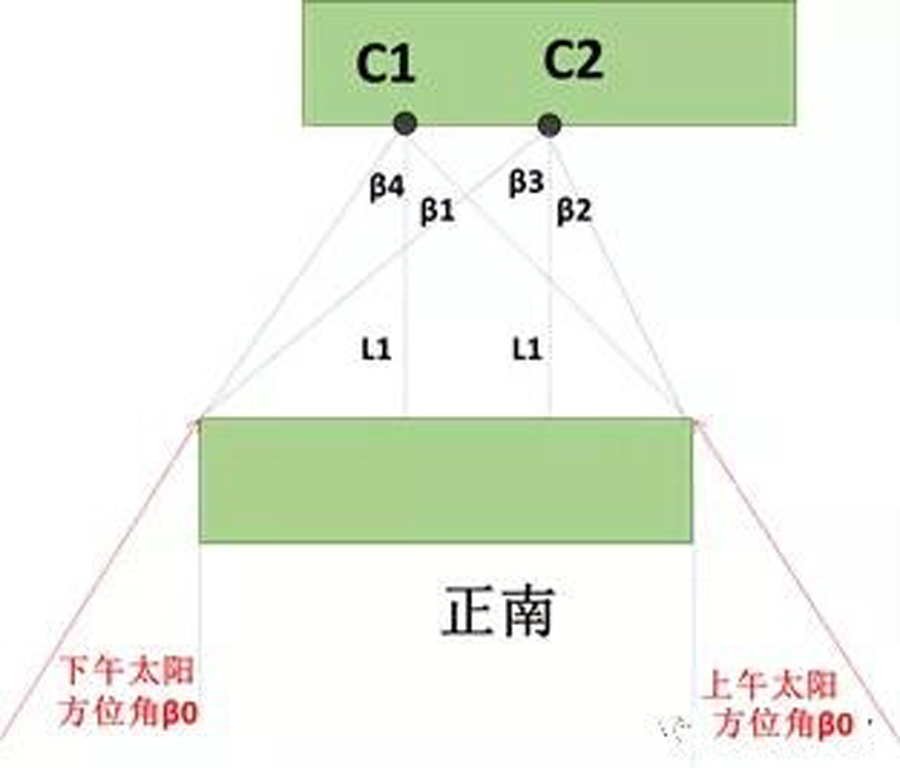
其中,β1=47°,β2=25°,β3=52°,β4=29°
请分析,假设冬至日全天晴朗,小王的阳台在冬至日那天能够照射到多久的太阳?
解答:
韶关市冬至日正午高度角为41.7°为已知。
首先判断实际楼距是否达到理论不遮挡的小楼距。理论楼距L= 40/tan(41.7°)= 43.88米;而小王所住楼和阳台对面楼实际楼距只有20米,因此必然小王所在的楼宇的低楼层必然长期会受到影子遮挡;
接下来,要看看小王坐住的楼层阳台的遮挡情况;
前面计算冬至日那天不同时点的太阳高度角、方位角、临界高度等等概念不再一一赘述,直接上图表进行分析
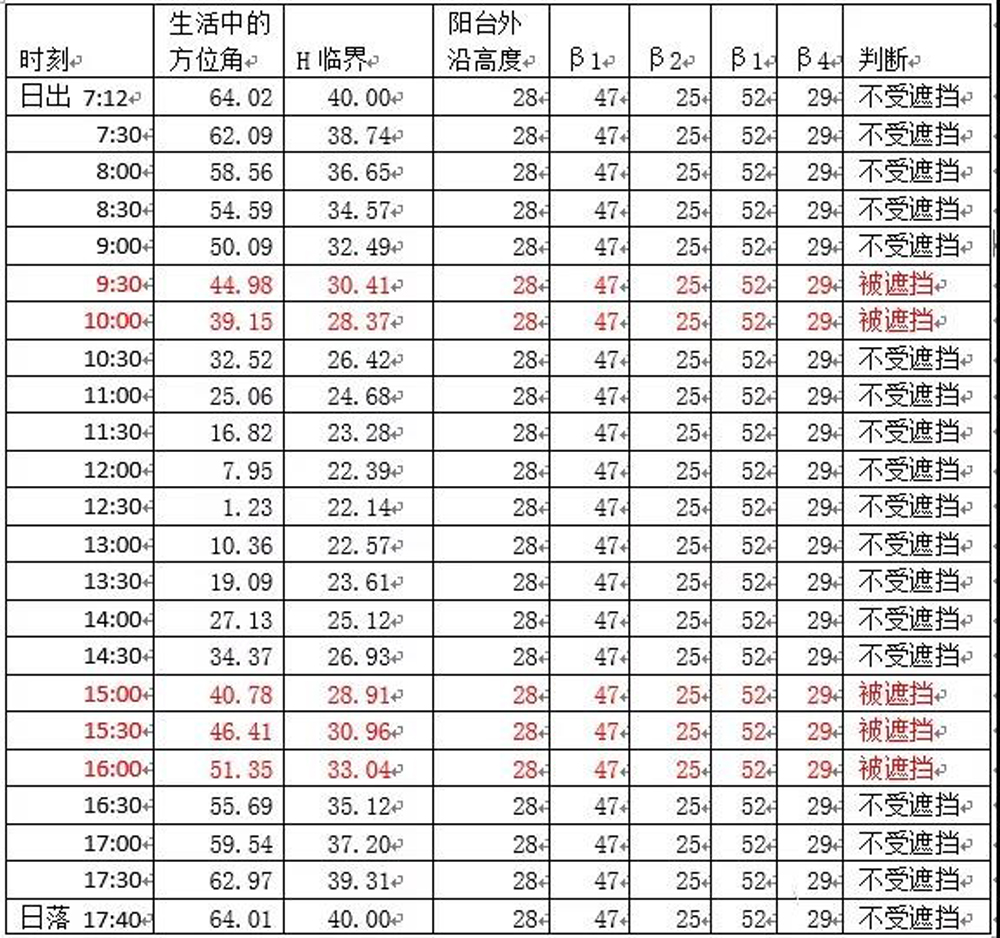
在上表的右列,我用了if….else,或者IF() 的函数,很容易就判断出了小王阳台被遮挡的时间段。上表这5个标红的时间段就是阳台被遮挡,当然我在这里用了半小时为间隔,如果用10分钟或者更细的话,可以计算得更细致一些。
根据之前设置的上午10:00到下午16:00的有效照射时段来看,小王的阳台在上午不到半小时,下午有1个半小时是会有太阳遮挡的。总计被遮挡的时间有2小时左右,占整个6小时有效时段的1/3,可以说也还是不错的了。是不是很方便?
小结:上面讲了长长的分析过程,看的让人眼花缭乱,也有可能会让人头晕脑胀。下面需要做一下总结:
步:如果你时间充裕,或者多装几个摄像头,通过记录任何日子下的阳台被太阳光照时间,了解阳台是否被遮挡;或者,如果你有商业卫星公司的资源,可以查看特定日子,例如冬至日及前后几天的卫星图片,也可以准确的知道在一年中白昼短的日子里,阳台能够被太阳光照的时间;其他日期里,阳台受光照的时间只会比冬至日久。如果以上两个条件都不具备,那么可以考虑烧脑的下一步。
第二步:考虑太阳高度角及太阳方位角,测算冬至日当天阳台被有效光照的时间。以下是动作分解:
1、通过百度地图或谷歌地图、高德地图……,精确测量所在小区的经度和纬度。这次我用了韶关市区的经度纬度,主要是为了取整方便;
2、得到上面的数据后,利用赤纬、时角、时差分别计算出冬至日当天各个整点时段的太阳高度角θ、太阳方位角β。做好做一个表格,方便对比;
3、测量自己住的楼房和对面楼房的楼距、对面楼房的高度、阳台外沿高度、阳台外沿两端和对面楼房形成的夹角β1、β2、β3、β4;
4、上一步测量完之后,计算阳台外沿高度的临界值H临界;并根据第2步得到的各时点的太阳方位角β,和β1、β2、β3、β4进行对比,判断阳台是否受到遮挡,如果受到遮挡,那么反算出被遮挡的时间段;
5、利用第2步得到的各时点的太阳高度角θ,计算各时段影子上沿在自己住的楼房外立面的高度H, 并用之与H临界进行对比,修正第4步的结果。












